Just for fun——一个高中及格水平傻瓜式计算概率的实例

虽然猜雷中有很多简单的1/2或者2/3概率，不过偶尔也会出现不那么好确定概率的局面。

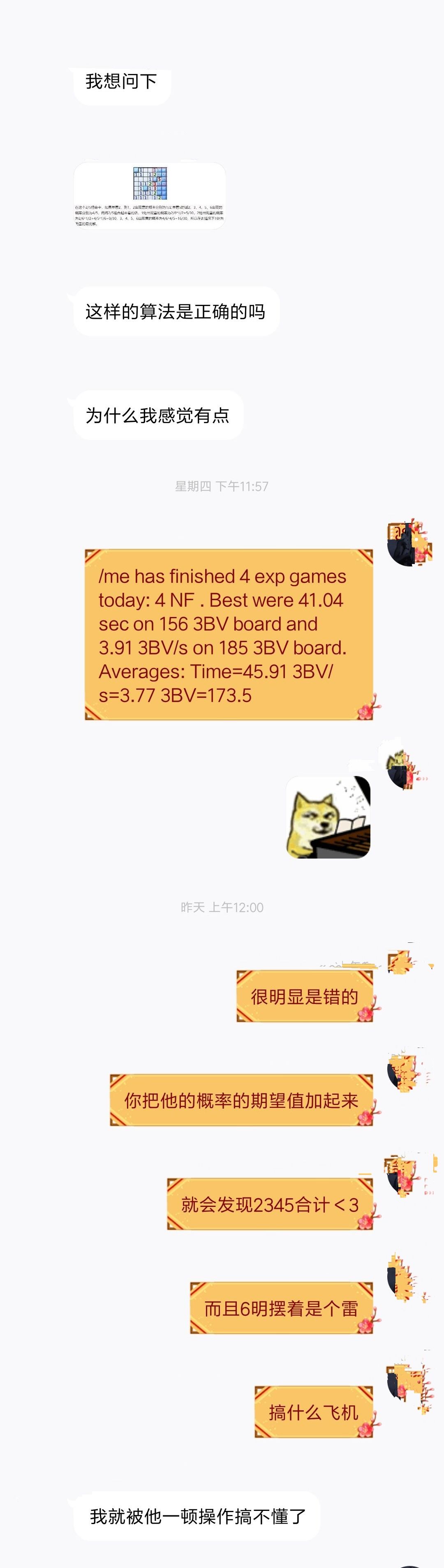
本文的想法来源于与群友聊天的内容，至于截图中的原计算者就不知道是哪位知乎大神了，如下图：

读过高中的人就能看出来槽点显而易见：

为了减少变量，我们将局面简化为：

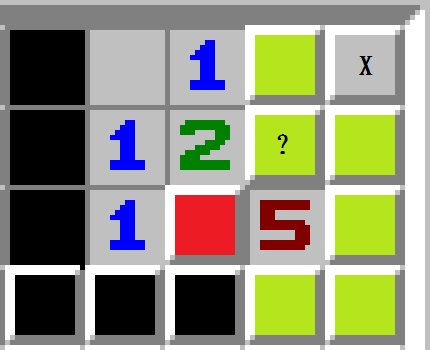
假定这个局部处于扫雷图右上角，标红为已知雷，因为已知雷的影响，涂黑区域均不是雷，但我们不去考虑涂黑局部翻开后的情况，只作为无雷的空腔放置。显然被包起来的右上角X并不能纳入计算范围，它与扫雷图剩余的区域(未在图上显示)等价。

荧光黄区域的总雷数实际上是不固定的，这也是这个概率计算唯一的问题。

假设?处为雷，则整个荧光黄区域的总雷数为4，记为P(4);若?处不为雷，则整个荧光黄区域的总雷数为5，记为P(5)。

显然P(4) + P(5) = 1。我们需要计算出P(4)和P(5)的比值。

当已经出现这种局部的时候，标红的雷和已知的空腔已经是锁定的，我们只需要考虑荧光黄区域和扫雷图剩余区域的组合数。设P(4)的组合数为A(4)，P(5)的组合数为A(5)，显然P(4) / P(5) = A(4) /A(5)。假设扫雷图剩余区域M格，总雷数N。

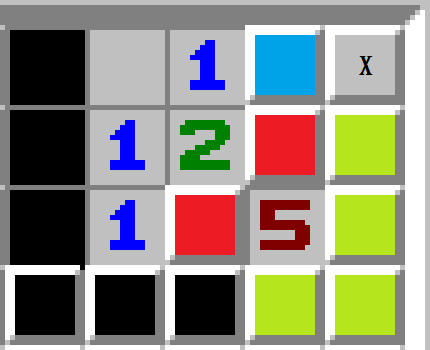
如上图，当?处是雷的时候，又有一个雷和一个空被锁定，需要排列的只有荧光黄区域内3雷及扫雷图剩余区域M格里面的N-5个雷。

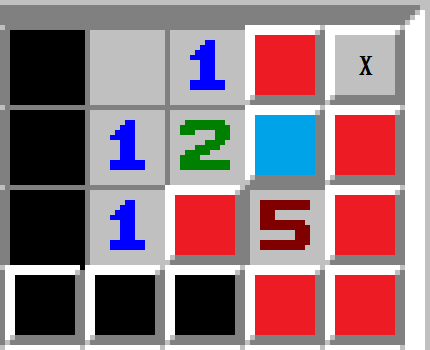
如上图，当?处不是雷的时候，整个局部都被锁定了，需要排列的只有扫雷图剩余区域M格里面的N-6个雷。简单计算如下：

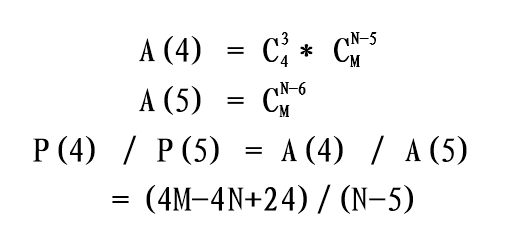
假设这是一张高级图，那么M=461，N=99

P(4) + P(5) = 1，P(4) / P(5) ≈ 15.66

不用算了……

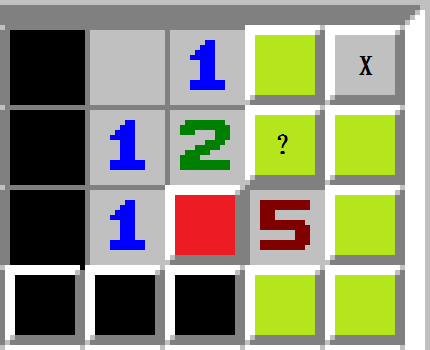
只考虑在高级里看到这个局部的情况下，?处是雷的概率，即P(4)，显然超过90%。

之前我们的扫雷经验一般描述为：一个局部的雷数会倾向于总数较少的方式排布，因为高级图雷的密度只有0.20625，很多种猜雷经验(比如拐角猜)都是按照雷数较少的方式去猜。实际算一下，确实符合预期。但如果雷的密度越来越大，大到M和N差值很小，那么该局部就会逐渐倾向于总雷数较多的分布。

这种计算是不够严密的，但结论应该问题不大。为什么要限定很多条件用傻瓜式算法呢?因为作者是个数学白痴(笑)。